Structural plasticity

#!pip install ANNarchy

As simple example showing how to use structural plasticity (creation/pruning of synapses) in a rate-coded network (spiking networks work similarly).

import numpy as np
import matplotlib.pyplot as plt

import ANNarchy as ann

ANNarchy 5.0 (5.0.0) on darwin (posix).

We define a leaky integrator rate-coded neuron and a small population:

LeakyIntegratorNeuron = ann.Neuron(
    parameters = dict(
        tau = 10.0 ,
        baseline = ann.Parameter(0.0),
    ),
    equations = [
        ann.Variable("tau * dr/dt + r = baseline", min=0.0),
    ]
)

net = ann.Network()

pop = net.create(50, LeakyIntegratorNeuron)

Structural plasticity has two components: creation of synapses and pruning (removal) under certain conditions. These conditions are defined in the synapse type itself in the pruning and creating arguments:

StructuralPlasticSynapse = ann.Synapse(
    parameters = dict(T = ann.Parameter(10000, type='int')),
    
    equations = ann.Variable(
        "age = if pre.r * post.r > 1.0 : 0 else : age + 1", 
        init = 0, 
        type=int
    ),
    
    pruning = ann.Pruning("age > T", proba = 0.1),
    
    creating = ann.Creating("pre.r * post.r > 1.0", proba = 0.5, w = 0.01),
)

proj = net.connect(pop, pop, 'exc', StructuralPlasticSynapse)
proj.fixed_probability(weights = 0.01, probability=0.1)

<ANNarchy.core.Projection.Projection at 0x13a4c2420>

These conditions must be boolean values, which when True may trigger the creation/pruning of a synapse. The flag proba gives the probability by which the synapse will actually be created/pruned.

• When creating is True, a synapse that did not exist will be created with the provided probability. Its weight will take the value provided by the flag w (0.01), the other variables take their default value.
• When pruning is True, a synapse that exists will be deleted with the given probability.

The pruning condition can depend on any pre-synaptic, post-synaptic or synaptic variable. The creating condition can only depend on pre- or post-synaptic conditions, as the synapse does not exist yet.

Apart from these two fields, the synapse is a regular synapse, one could also define synaptic plasticity mechanisms and so on.

We finally create a sparse projection within the population, with 10% connectivity.

net.compile()

The creation and pruning have to be explicitly started before a simulation, as they are very expensive computationally. The period argument states how often the conditions will be checked (avoid using dt):

# Start structural plasticity
proj.start_creating(period=100.0)
proj.start_pruning(period=100.0)

# Save the initial connectivity matrix
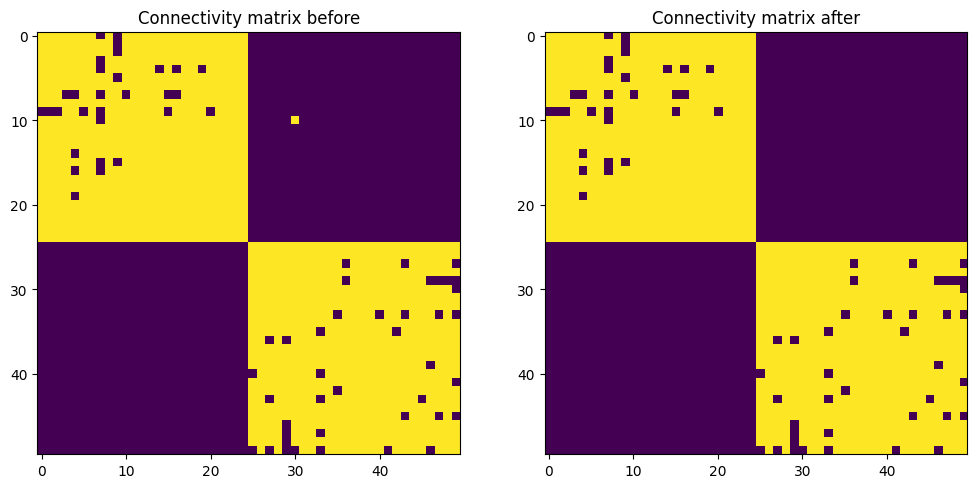
initial_weights = proj.connectivity_matrix()

To see the effect of structural plasticity, one alternatively activates one half of the population by setting a high baseline (mimicking corrrelated inputs). As neurons in one half will be activated at the same time, they will create synapses between each other. Between the two halves, the neurons are never co-activated, so the existing synapses will slowly die out.

# Let structural plasticity over several trials
for trial in range(20):
    
    # Activate the first subpopulation
    pop[:25].baseline = ann.Uniform(0.5, 1.5)
    
    # Simulate for 1s
    net.simulate(1000.)
    
    # Reset the population
    pop.baseline = 0.0
    net.simulate(100.)
    
    # Activate the second subpopulation
    pop[25:].baseline = ann.Uniform(0.5, 1.5) 
    
    # Simulate for 1s
    net.simulate(1000.)
    
    # Reset the population
    pop.baseline = 0.0
    net.simulate(100.)

# Inspect the final connectivity matrix
final_weights = proj.connectivity_matrix()

We can check the effect of structural plasticity by looking at the connectivity matrix before and after the stimulation:

plt.figure(figsize=(12, 8))
plt.subplot(121)
plt.imshow(initial_weights)
plt.title('Connectivity matrix before')
plt.subplot(122)
plt.imshow(final_weights)
plt.title('Connectivity matrix after')
plt.show()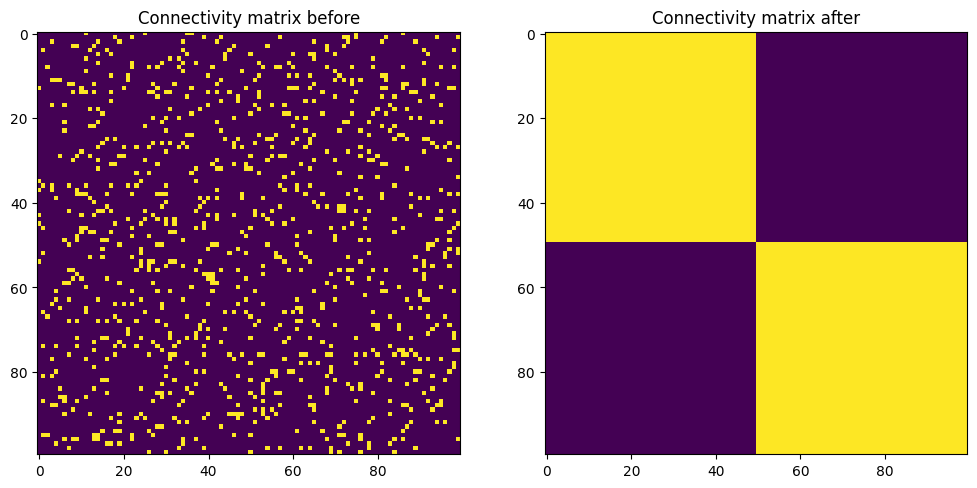

Synapses can be also created/pruned externally from python, using Dendrite.create_synapse() and Dendrite.prune_synapse().

Here we add a single synapse in a quadrant of the connectivity matrix where no synapses existed:

# Add a synapse
proj.dendrite(10).create_synapse(rank=30, w=0.01)

# Inspect the final connectivity matrix
weights_after_insertion = proj.connectivity_matrix()

plt.figure(figsize=(12, 8))
plt.subplot(121)
plt.imshow(final_weights)
plt.title('Connectivity matrix before')
plt.subplot(122)
plt.imshow(weights_after_insertion)
plt.title('Connectivity matrix after')
plt.show()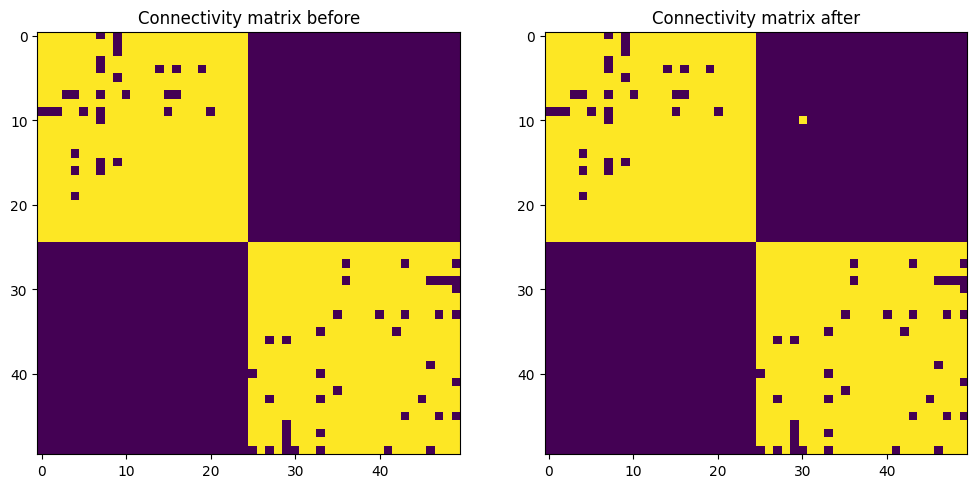

# Remove the synapse
proj.dendrite(10).prune_synapse(rank=30)

# Inspect the final connectivity matrix
weights_after_deletion = proj.connectivity_matrix()

plt.figure(figsize=(12, 8))
plt.subplot(121)
plt.imshow(weights_after_insertion)
plt.title('Connectivity matrix before')
plt.subplot(122)
plt.imshow(weights_after_deletion)
plt.title('Connectivity matrix after')
plt.show()