Neural Field

Download JupyterNotebook Download JupyterNotebook

#!pip install ANNarchy

This notebook demonstrates a simple rate-coded model using Neural Fields. It consists of two 2D populations inp and pop, with one-to-one connections between inp and pop, and Difference-of-Gaussians (DoG) lateral connections within pop.

It is is based on the following paper:

Nicolas P. Rougier and Julien Vitay (2005). Emergence of attention within a neural population. Neural Networks 19(5). doi:10.1016/j.neunet.2005.04.004

Model overview

Each population consists of N*N neurons, with N=20. The inp population is solely used to represent inputs for pop. The pop population implements a discretized neural field, with neurons following the ODE:

\tau \frac{d r_i(t)}{dt} + r_i(t) = r^\text{input}_i(t) + \sum_{j=1}^{N} w_{j, i} \cdot r_j(t) + \eta(t)

where r_i(t) is the neuron’s firing rate, \tau a time constant and w_{j, i} the weight value (synaptic efficiency) of the synapse between the neurons j and i. \eta(t) is an additive noise uniformly taken in [-0.5, 0.5]. f() is a semi-linear function, ensuring the firing rate is bounded between 0 and 1.

Each neuron in pop takes inputs from the neuron of inp which has the same position, leading to a one_to_one connection pattern.

The lateral connections within pop follow a difference-of-Gaussians (dog) connection pattern, with the connection weights w_{i,j} depending on the normalized euclidian distance between the neurons in the N*N population:

w_{j, i} = A^+ \cdot \exp(-\frac{1}{2}\frac{d(i, j)^2}{\sigma_+^2}) - A^- \cdot \exp(-\frac{1}{2}\frac{d(i, j)^2}{\sigma_-^2})

If i and j have coordinates (x_i, y_i) and (x_j, y_j) in the N*N space, the distance between them is computed as:

d(i, j)^2 = (\frac{x_i - x_j}{N})^2 + (\frac{y_i - y_j}{N})^2

Inputs are given to the network by changing the firing rate of inp neurons.

Importing ANNarchy

We first start by importing the numpy and ANNarchy libraries:

import numpy as np
import matplotlib.pyplot as plt

import ANNarchy as ann
ANNarchy 4.8 (4.8.2) on darwin (posix).

The setup() method allows to configure ANNarchy to run in different modes, such as chosing the parallel framework (omp or cuda), setting the simulation step dt, the numerical method method or the seed of the random number generators.

Defining the neuron

NeuralFieldNeuron = ann.Neuron(
    parameters=""" 
        tau = 10.0 : population
    """,
    equations="""
        tau * dr/dt + r = sum(exc) + sum(inh) + Uniform(-0.5, 0.5) : min=0.0, max=1.0
    """
)

The NeuralField neuron is governed by an ODE and considers inputs from other neurons. It has a non-linear activation function, which is linear when the firing rate is between 0.0 and 1.0, and constant otherwise.

tau is a population-wise parameter, whose value will be the same for all neuron of the population.

r is the firing rate of he neuron, whose dynamics are governed by a first-order linear ODE, integrating the sums of excitatory and inhibitory inputs with noise.

As explained in the manual for rate-coded neurons, sum(exc) retrieves the weighted sum of pre-synaptic firing rates for the synapses having the connection type exc, here the one_to_one connections between inp and pop. sum(inh) does the same for inh type connections, here the lateral connections within pop.

The firing rate is restricted to the range [0, 1] by setting the min and max accordingly in the flags section (everything after the :). This means that after evaluating the ODE and getting a new value for r, its value will be clamped if it outside these values. One can define both min and max, only one, or none.

Creating the populations

The two populations have a geometry of (20, 20), therefore 400 neurons each. They are created simply by instantiating the Population class:

N = 20
inp = ann.InputArray(geometry = (N, N), name='Input')
pop = ann.Population(geometry = (N, N), neuron = NeuralFieldNeuron, name='Focus')

The populations can be assigned a unique name (here ‘Input’ and ‘Focus’) in order to be be able to retrieve them if the references inp and focus are lost. They are given a 2D geometry and associated to the corresponding Neuron instance.

Creating the projections

The first projection is a one-to-one projection from Input to Focus with the type ‘exc’. This connection pattern pattern is possible because the two populations have the same geometry. The weights are initialized to 1.0, and this value will not change with time (no learning), so it is not necessary to define a synapse type:

ff = ann.Projection(pre=inp, post=pop, target='exc')
ff.connect_one_to_one(weights=1.0, delays = 20.0)
<ANNarchy.core.Projection.Projection at 0x116db8830>

The references to the pre- and post-synaptic population (or their names), as well as the target type, are passed to the constructor of Projection. The connector method connect_one_to_one() is immediately applied to the Projection, defining how many synapses will be created. The weights are initialized uniformly to 1.0.

The second projection is a difference of gaussians (DoG) for the lateral connections within pop. The connector method is already provided by ANNarchy, so there is nothing more to do than to call it with the right parameters:

lat = ann.Projection(pre=pop, post=pop, target='inh')
lat.connect_dog(amp_pos=0.2, sigma_pos=0.1, amp_neg=0.1, sigma_neg=0.7)
<ANNarchy.core.Projection.Projection at 0x116ce60d0>

We set two monitors recording the firing rate of the two populations:

m = ann.Monitor(inp, 'r')
n = ann.Monitor(pop, 'r')

Compiling the network and simulating

Once the populations and projections are created, the network is ready to be generated, compiled and simulated. Compilation is simply done by calling compile():

ann.compile()
Compiling ...  OK

This generates optimized C++ code from the neurons’ definition and network structure, compiles it with gcc/clang and instantiates all objects, particularly the synapses. If some errors were made in the neuron definition, they will be signaled at this point.

Hint: The call to compile() is mandatory in any script. After it is called, populations and projections can not be added anymore.

Once the compilation is successful, the network can be simulated by calling simulate(). As no input has been fed into the network yet, calling simulate() now won’t lead to anything interesting. The next step is to clamp inputs into the input population’s baseline.

Setting inputs

Tight loop

In this example, we use a moving bubble of activity rotating along a circle in the 20*20 input space in 1 second (i.e. 1000 steps). The simplest way of setting such inputs is to access population attributes (namely inp.r) in a tight loop in Python:

def gaussian(angle):
    "Unnormalized Gaussian at the specified angle."
    # 20*20 matrices with XY coordinates
    xx, yy = np.meshgrid(np.linspace(0, N-1, N), np.linspace(0, N-1, N))

    # Compute the center of the bubble
    cx = N / 2. * ( 1.0 + 0.5 * np.cos(2.0 * np.pi * angle ) )
    cy = N / 2. * ( 1.0 + 0.5 * np.sin(2.0 * np.pi * angle ) )

    # Gaussian
    bubble = np.exp(-((xx-cx)**2 + (yy-cy)**2)/8.0)
    return bubble

# Main loop
T = 1000
angle = 0.0
for t in range(T):

    # Update the angle
    angle += 1.0/T
    
    # Clamp the firing rate of inp with the Gaussian and some noise
    inp.r = gaussian(angle) + np.random.uniform(-0.5, 0.5, (N, N))
    
    # Simulate for one step = 1 ms
    ann.step()

angle represents the angle made by the bubble with respect to the center of the input population. At each iteration of the simulation (i.e. every millisecond of simulation), the bubble is slightly rotated (angle is incremented) so as to make a complete revolution in 1 seconds (1000 steps).

A Gaussian function (in the form of the Numpy array returned by the gaussian() methpd) is then clamped into the activity of inp. Some uniform noise is then added.

Last, a single simulation step is performed using step(). step() is equivalent to simulate(dt), although a little bit faster as it does not check anything.

Let’s plot the firing rates of the two populations at the end of the simulation:

plt.figure(figsize=(15, 10))
plt.subplot(121)
plt.imshow(inp.r, interpolation='nearest', cmap=plt.cm.gray)
plt.subplot(122)
plt.imshow(pop.r, interpolation='nearest', cmap=plt.cm.gray)
plt.show()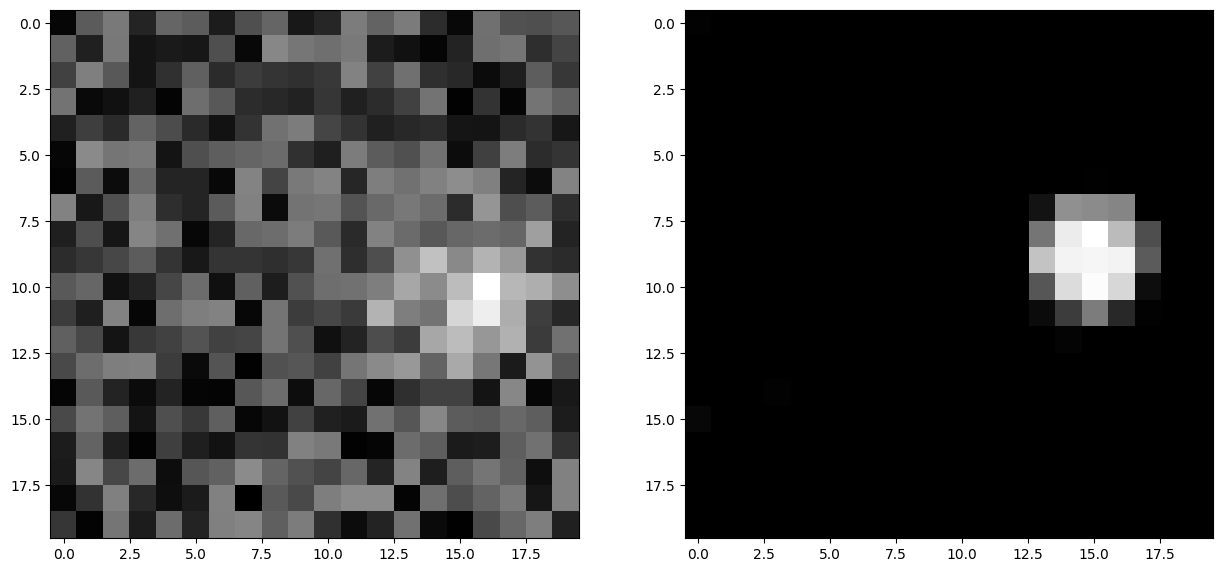

We see a noisy bubble of activity in inp and a clean one in pop, demonstrating the noise-filtering capacities of neural fields.

Let’s retrieve the data recorded by the monitors, and use Matplotlib animations to show how the firing rates changed during the simulation (other methods are possible):

inp_data = m.get('r')
pop_data = n.get('r')
%matplotlib inline
from matplotlib import animation
from IPython.display import HTML

fig = plt.figure(figsize=(10,5))
ax1 = plt.subplot(1,2,1)   
ax2 = plt.subplot(1,2,2)

im1 = ax1.imshow(inp.r, interpolation='nearest', cmap=plt.cm.gray)
im2 = ax2.imshow(pop.r, interpolation='nearest', cmap=plt.cm.gray)

def drawframe(n):
    im1.set_data(inp_data[n].reshape((N, N)))
    im2.set_data(pop_data[n].reshape((N, N)))    
    return (im1, im2)

anim = animation.FuncAnimation(fig, drawframe, frames=T, interval=2, blit=True)
plt.close()
HTML(anim.to_html5_video())

Everything works as expected. However, the simulation is actually quite slow (even if you do not notice it here), as Python is bad at tight loops like this one. For longer simulations, the overhead of python might become too damaging.

TimedArray

A much more efficient variant is to precompute the input rates and store them in an array that will be iteratively read by the TimedArrayobject. This is a new population that unfortunately cannot be added to the network anymore, as we have already compiled it. Let’s clear the network and redefine everything, replacing the InputArray with a TimedArray of the same shape:

ann.clear()

NeuralFieldNeuron = ann.Neuron(
    parameters="tau = 10.0 : population",
    equations="tau * dr/dt + r = sum(exc) + sum(inh) + Uniform(-0.5, 0.5) : min=0.0, max=1.0")

N = 20
inp = ann.TimedArray(geometry = (N, N), name='Input')
pop = ann.Population(geometry = (N, N), neuron = NeuralFieldNeuron, name='Focus')

ff = ann.Projection(pre=inp, post=pop, target='exc')
ff.connect_one_to_one(weights=1.0, delays = 20.0)

lat = ann.Projection(pre=pop, post=pop, target='inh')
lat.connect_dog(amp_pos=0.2, sigma_pos=0.1, amp_neg=0.1, sigma_neg=0.7)

m = ann.Monitor(inp, 'r')
n = ann.Monitor(pop, 'r')

ann.compile()

We now create a numpy array of shape (T, N, N) where T is the duration of the simulation (1000 steps) and N the dimension of the neural field. We make sure to add noise to the inputs.

We then set the rates parameter of the TimedArrayto that array by using update(). At each step of the simulation, the timed array will “read” a new input activity in that array and store it as r. We simply need to call simulate()for the whole duration of the simulation, instead of using a slow tight loop in Python.

def gaussian(angle):
    "Unnormalized Gaussian at the specified angle."
    # 20*20 matrices with XY coordinates
    xx, yy = np.meshgrid(np.linspace(0, N-1, N), np.linspace(0, N-1, N))

    # Compute the center of the bubble
    cx = N / 2. * ( 1.0 + 0.5 * np.cos(2.0 * np.pi * angle ) )
    cy = N / 2. * ( 1.0 + 0.5 * np.sin(2.0 * np.pi * angle ) )

    # Gaussian
    bubble = np.exp(-((xx-cx)**2 + (yy-cy)**2)/8.0)
    return bubble

# Precompute the angles for 1000 steps = 1 cycle
T = 1000
angles = np.linspace(0, 1, T)

# Accumulate the 1000 inputs with time as the first dimension
input_rates = np.array([gaussian(angle) + np.random.uniform(-0.5, 0.5, (N, N)) for angle in angles])

# Set it as the rates argument of the input population
inp.update(input_rates)

# Simulate for 1 second
ann.simulate(T)

# Retrieve the recordings
inp_data = m.get('r')
pop_data = n.get('r')
%matplotlib inline
from matplotlib import animation
from IPython.display import HTML

fig = plt.figure(figsize=(10,5))
ax1 = plt.subplot(1,2,1)   
ax2 = plt.subplot(1,2,2)

im1 = ax1.imshow(inp.r, interpolation='nearest', cmap=plt.cm.gray)
im2 = ax2.imshow(pop.r, interpolation='nearest', cmap=plt.cm.gray)

def drawframe(n):
    im1.set_data(inp_data[n].reshape((N, N)))
    im2.set_data(pop_data[n].reshape((N, N)))    
    return (im1, im2)

anim = animation.FuncAnimation(fig, drawframe, frames=T, interval=2, blit=True)
plt.close()
HTML(anim.to_html5_video())