Short-term Plasticity and Synchrony

Download JupyterNotebook Download JupyterNotebook

#!pip install ANNarchy

Implementation of the recurrent network with short-term plasticity (STP) proposed in:

Tsodyks, Uziel and Markram (2000). Synchrony Generation in Recurrent Networks with Frequency-Dependent Synapses, The Journal of Neuroscience, 20(50).

import numpy as np
import matplotlib.pyplot as plt
import ANNarchy as ann
ANNarchy 5.0 (5.0.0) on darwin (posix).

This network uses simple leaky integrate-and-fire (LIF) neurons:

LIF = ann.Neuron(
    parameters = dict(
        tau = 30.0,
        I = ann.Parameter(15.0),
        tau_I = 3.0,
    ),
    equations = [
        ann.Variable('tau * dv/dt = -v + g_exc - g_inh + I', init=13.5),
        ann.Variable('tau_I * dg_exc/dt = -g_exc'),
        ann.Variable('tau_I * dg_inh/dt = -g_inh'),
    ],
    spike = "v > 15.0",
    reset = "v = 13.5",
    refractory = 3.0
)

net = ann.Network(dt=0.25)

P = net.create(geometry=500, neuron=LIF)
P.I = np.sort(ann.Uniform(14.625, 15.375).get_values(500))
P.v = ann.Uniform(0.0, 15.0)
Exc = P[:400]
Inh = P[400:]

Short-term plasticity can be defined by dynamical changes of synaptic efficiency, based on pre- or post-synaptic activity.

We define a STP synapse, whose post-pynaptic potential (psp, define by g_target) depends not only on the weight w and the emission of pre-synaptic spike, but also on intra-synaptic variables x and u:

STP = ann.Synapse(
    parameters = dict(
        tau_rec = ann.Parameter(1.0),
        tau_facil = ann.Parameter(1.0),
        U = ann.Parameter(0.1),
    ),
    equations = [
        ann.Variable('dx/dt = (1 - x)/tau_rec', init = 1.0, method='event-driven'),
        ann.Variable('du/dt = (U - u)/tau_facil', init = 0.1, method='event-driven'),
    ],
    pre_spike="""
        g_target += w * u * x
        x *= (1 - u)
        u += U * (1 - u)
    """
)

Creating the projection between the excitatory and inhibitory is straightforward when the right parameters are chosen:

# Parameters for the synapses
Aee = 1.8
Aei = 5.4
Aie = 7.2
Aii = 7.2

Uee = 0.5
Uei = 0.5
Uie = 0.04
Uii = 0.04

tau_rec_ee = 800.0
tau_rec_ei = 800.0
tau_rec_ie = 100.0
tau_rec_ii = 100.0

tau_facil_ie = 1000.0
tau_facil_ii = 1000.0

# Create projections
proj_ee = net.connect(pre=Exc, post=Exc, target='exc', synapse=STP)
proj_ee.fixed_probability(probability=0.1, weights=ann.Normal(Aee, (Aee/2.0), min=0.2*Aee, max=2.0*Aee)) 
proj_ee.U = ann.Normal(Uee, (Uee/2.0), min=0.1, max=0.9)
proj_ee.tau_rec = ann.Normal(tau_rec_ee, (tau_rec_ee/2.0), min=5.0)
proj_ee.tau_facil = net.dt # Cannot be 0!

proj_ei = net.connect(pre=Inh, post=Exc, target='inh', synapse=STP)
proj_ei.fixed_probability(probability=0.1, weights=ann.Normal(Aei, (Aei/2.0), min=0.2*Aei, max=2.0*Aei))
proj_ei.U = ann.Normal(Uei, (Uei/2.0), min=0.1, max=0.9)
proj_ei.tau_rec = ann.Normal(tau_rec_ei, (tau_rec_ei/2.0), min=5.0)
proj_ei.tau_facil = net.dt # Cannot be 0!

proj_ie = net.connect(pre=Exc, post=Inh, target='exc', synapse=STP)
proj_ie.fixed_probability(probability=0.1, weights=ann.Normal(Aie, (Aie/2.0), min=0.2*Aie, max=2.0*Aie))
proj_ie.U = ann.Normal(Uie, (Uie/2.0), min=0.001, max=0.07)
proj_ie.tau_rec = ann.Normal(tau_rec_ie, (tau_rec_ie/2.0), min=5.0)
proj_ie.tau_facil = ann.Normal(tau_facil_ie, (tau_facil_ie/2.0), min=5.0)

proj_ii = net.connect(pre=Inh, post=Inh, target='inh', synapse=STP)
proj_ii.fixed_probability(probability=0.1, weights=ann.Normal(Aii, (Aii/2.0), min=0.2*Aii, max=2.0*Aii))
proj_ii.U = ann.Normal(Uii, (Uii/2.0), min=0.001, max=0.07)
proj_ii.tau_rec = ann.Normal(tau_rec_ii, (tau_rec_ii/2.0), min=5.0)
proj_ii.tau_facil = ann.Normal(tau_facil_ii, (tau_facil_ii/2.0), min=5.0)

We compile and simulate for 10 seconds:

# Compile
net.compile()

# Record
Me = net.monitor(Exc, 'spike')
Mi = net.monitor(Inh, 'spike')

# Simulate
duration = 10000.0
net.simulate(duration, measure_time=True)
Compiling network 1...  OK 
Simulating 10.0 seconds of the network 1 took 0.07660222053527832 seconds.

We retrieve the recordings and plot them:

# Retrieve recordings
data_exc = Me.get()
data_inh = Mi.get()
te, ne = Me.raster_plot(data_exc['spike'])
ti, ni = Mi.raster_plot(data_inh['spike'])

# Histogram of the exc population
h = Me.histogram(data_exc['spike'], bins=1.0)

# Mean firing rate of each excitatory neuron
rates = []
for neur in data_exc['spike'].keys():
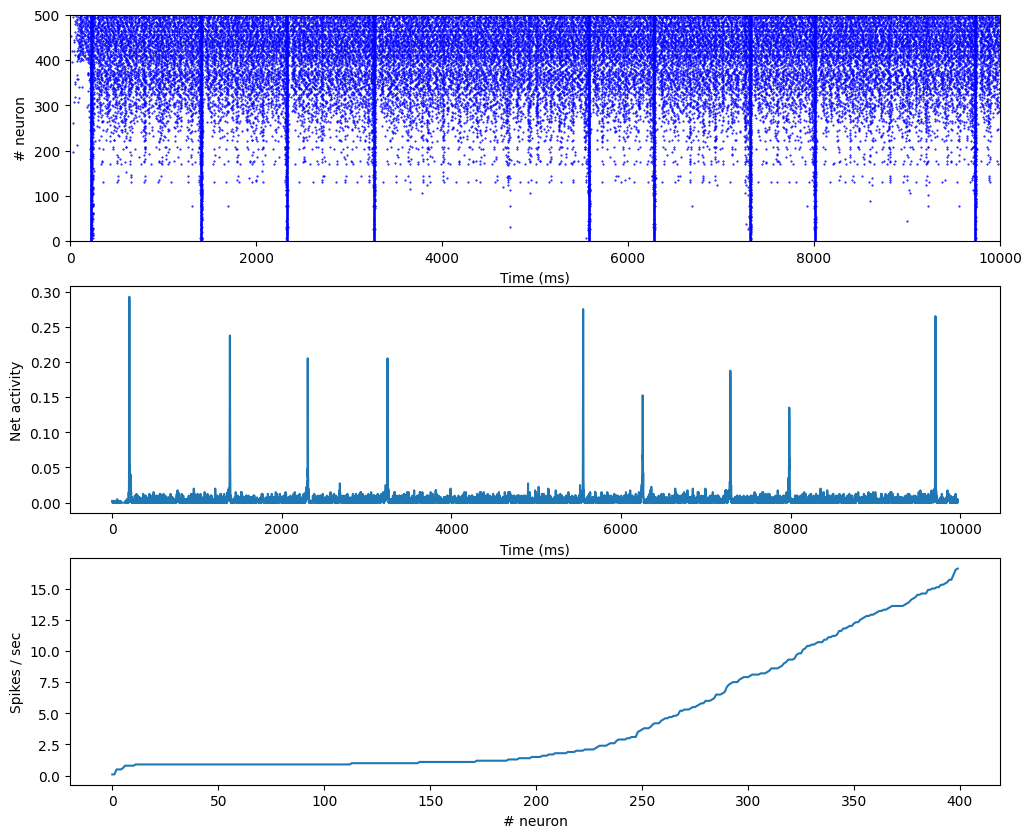
    rates.append(len(data_exc['spike'][neur])/duration*1000.0)
plt.figure(figsize=(12, 10))
plt.subplot(3,1,1)
plt.plot(te, ne, 'b.', markersize=1.0)
plt.plot(ti, ni, 'b.', markersize=1.0)
plt.xlim((0, duration)); plt.ylim((0,500))
plt.xlabel('Time (ms)')
plt.ylabel('# neuron')

plt.subplot(3,1,2)
plt.plot(h/400.)
plt.xlabel('Time (ms)')
plt.ylabel('Net activity')

plt.subplot(3,1,3)
plt.plot(sorted(rates))
plt.ylabel('Spikes / sec')
plt.xlabel('# neuron')
plt.show()