ANNarchy
Artificial Neural Networks architect
Outline
Neurocomputational models
Neuro-simulator ANNarchy
Rate-coded networks
Spiking networks
1 - Neurocomputational models
Computational neuroscience
Computational neuroscience is about explaining brain functioning at various levels (neural activity patterns, behavior, etc.) using biologically realistic neuro-computational models.
Different types of neural and synaptic mathematical models are used in the field, abstracting biological complexity at different levels.
There is no “right” level of biological plausibility for a model - you can always add more details -, but you have to find a paradigm that allows you to:
- Explain the current experimental data.
- Make predictions that can be useful to experimentalists.
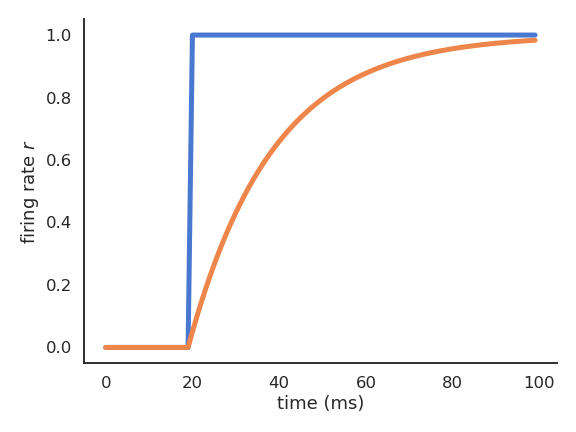
Rate-coded and spiking neurons
- Rate-coded neurons only represent the instantaneous firing rate of a neuron:
\tau \, \frac{d v(t)}{dt} + v(t) = \sum_{i=1}^d w_{i, j} \, r_i(t) + b
r(t) = f(v(t))
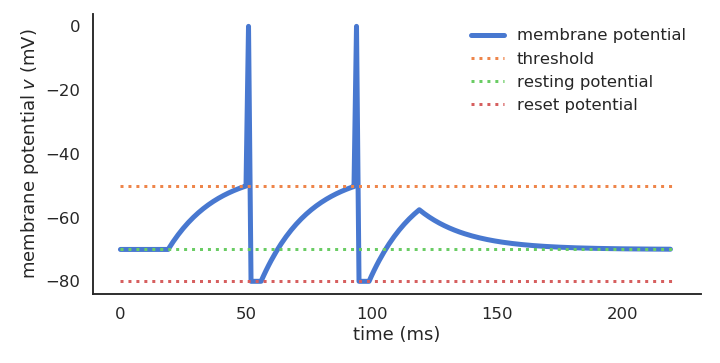
- Spiking neurons emit binary spikes when their membrane potential exceeds a threshold (leaky integrate-and-fire, LIF):
C \, \frac{d v(t)}{dt} = - g_L \, (v(t) - V_L) + I(t)
\text{if} \; v(t) > V_T \; \text{emit a spike and reset.}
Many different spiking neuron models are possible
- Izhikevich quadratic IF (Izhikevich, 2003).
\begin{cases} \displaystyle\frac{dv}{dt} = 0.04 \, v^2 + 5 \, v + 140 - u + I \\ \\ \displaystyle\frac{du}{dt} = a \, (b \, v - u) \\ \end{cases}
- Adaptive exponential IF (AdEx, Brette and Gerstner, 2005).
\begin{cases} \begin{aligned} C \, \frac{dv}{dt} = -g_L \ (v - E_L) + & g_L \, \Delta_T \, \exp(\frac{v - v_T}{\Delta_T}) \\ & + I - w \end{aligned}\\ \\ \tau_w \, \displaystyle\frac{dw}{dt} = a \, (v - E_L) - w\\ \end{cases}
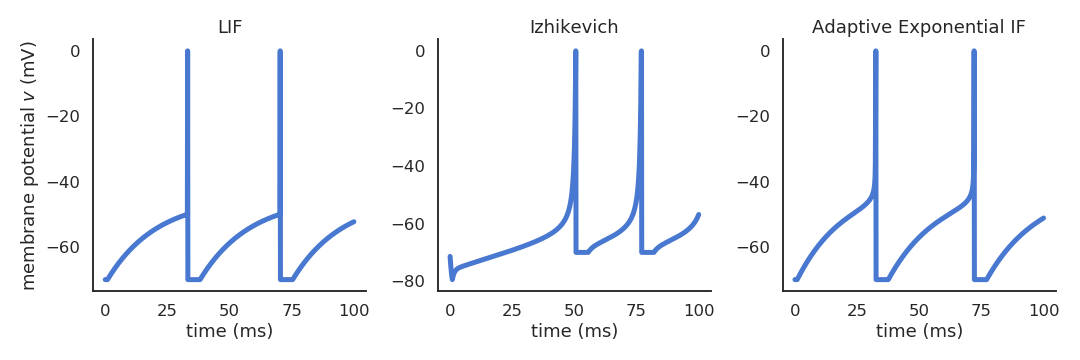
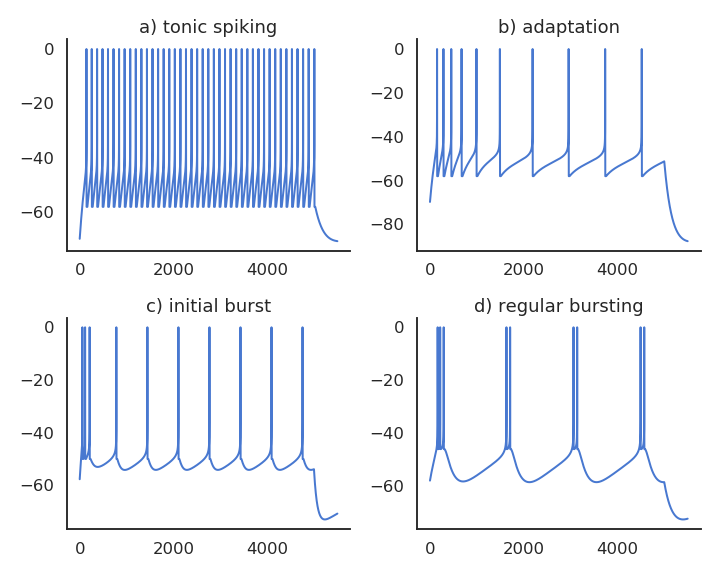
Realistic neuron models can reproduce a variety of dynamics
Biological neurons do not all respond the same to an input current: Some fire regularly, some slow down with time., some emit bursts of spikes…
Modern spiking neuron models allow to recreate these dynamics by changing just a few parameters.
Populations of neurons
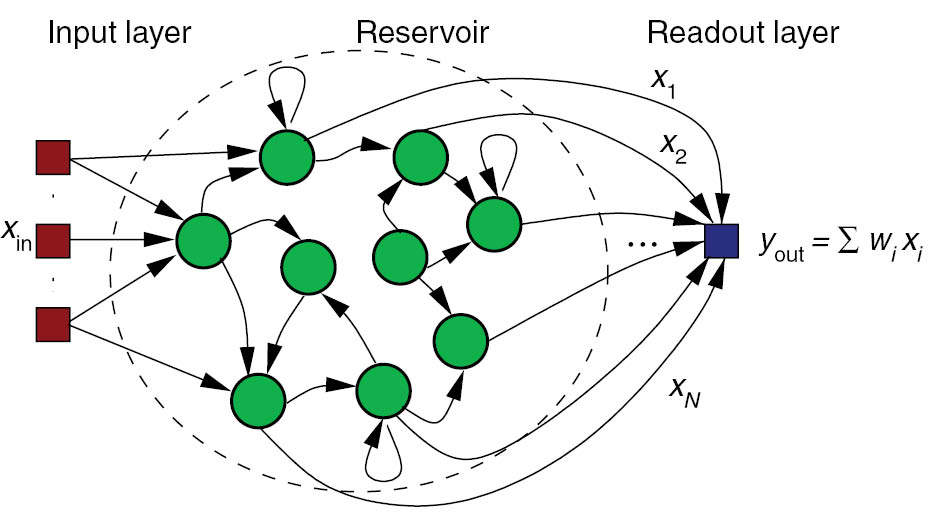
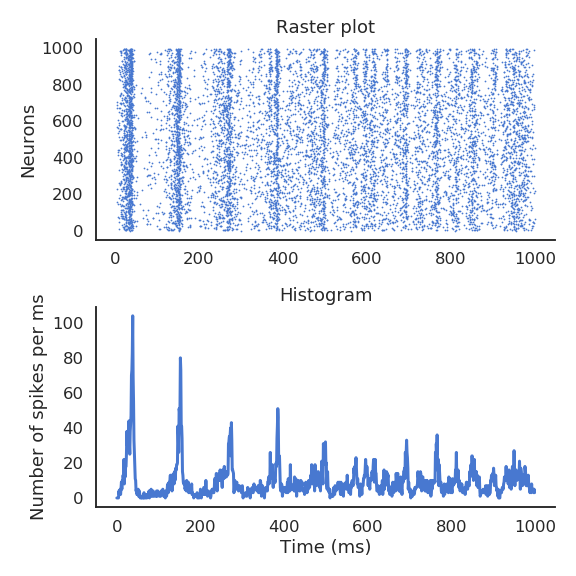
- Recurrent neural networks (e.g. randomly connected populations of neurons) can exhibit very rich dynamics even in the absence of inputs:
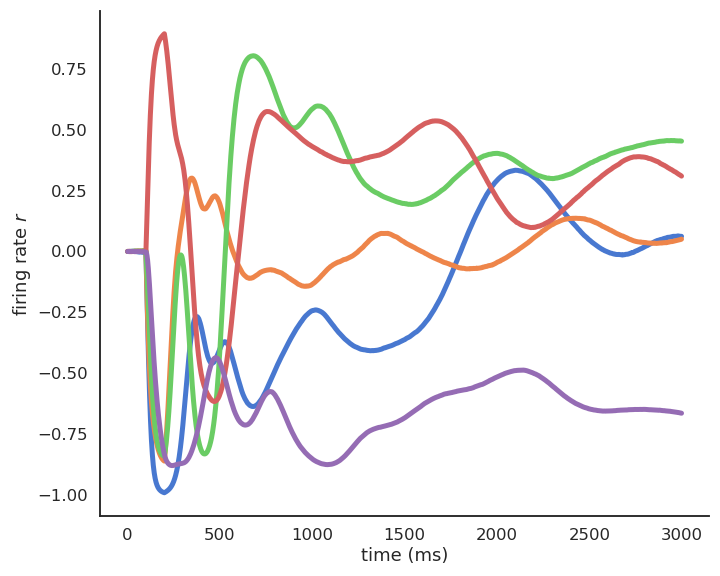
Oscillations at the population level.
Excitatory/inhibitory balance.
Spatio-temporal separation of inputs (reservoir computing).
Synaptic plasticity: Hebbian learning
- Hebbian learning postulates that synapses strengthen based on the correlation between the activity of the pre- and post-synaptic neurons:
When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.
Donald Hebb, 1949
- Weights increase proportionally to the the product of the pre- and post-synaptic firing rates:
\frac{dw}{dt} = \eta \, r^\text{pre} \, r^\text{post}
Synaptic plasticity: Hebbian-based learning
- The BCM (Bienenstock et al., 1982; Intrator and Cooper, 1992) plasticity rule allows LTP and LTD depending on the post-synaptic activity:
\frac{dw}{dt} = \eta \, r^\text{pre} \, r^\text{post} \, (r^\text{post} - \mathbb{E}[(r^\text{post})^2])
- Covariance learning rule (Dayan and Abbott, 2001):
\frac{dw}{dt} = \eta \, r^\text{pre} \, (r^\text{post} - \mathbb{E}[r^\text{post}])
- Oja learning rule (Oja, 1982):
\frac{dw}{dt}= \eta \, r^\text{pre} \, r^\text{post} - \alpha \, (r^\text{post})^2 \, w
or virtually anything depending only on the pre- and post-synaptic firing rates, e.g. Vitay and Hamker (2010):
\begin{aligned} \frac{dw}{dt} & = \eta \, ( \text{DA}(t) - \overline{\text{DA}}) \, (r^\text{post} - \mathbb{E}[r^\text{post}] )^+ \, (r^\text{pre} - \mathbb{E}[r^\text{pre}])- \alpha(t) \, ((r^\text{post} - \mathbb{E}[r^\text{post}] )^+ )^2 \, w \end{aligned}
STDP: Spike-timing dependent plasticity
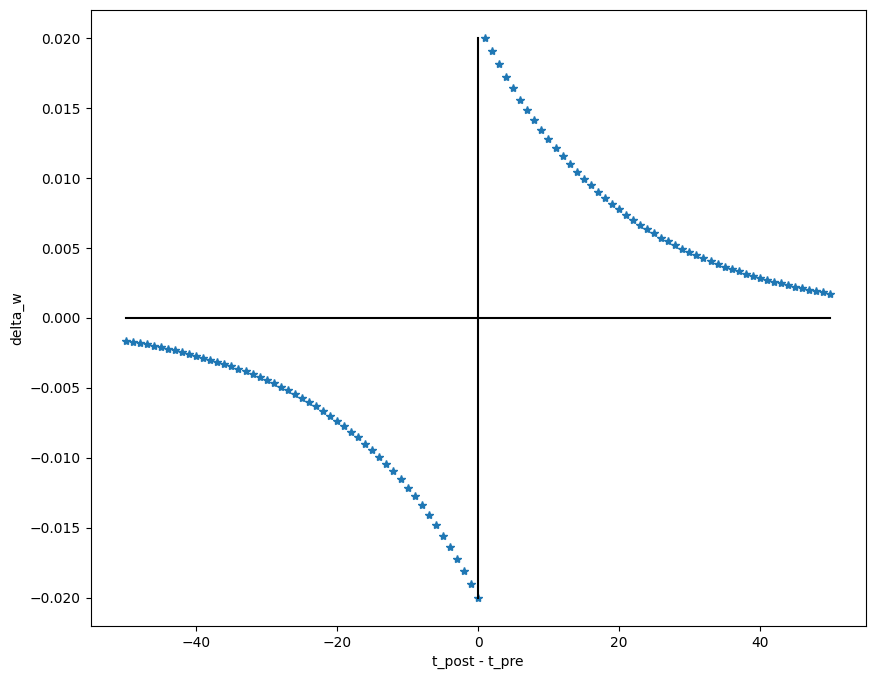
Synaptic efficiencies actually evolve depending on the the causation between the neuron’s firing patterns:
If the pre-synaptic neuron fires before the post-synaptic one, the weight is increased (long-term potentiation). Pre causes Post to fire.
If it fires after, the weight is decreased (long-term depression). Pre does not cause Post to fire.
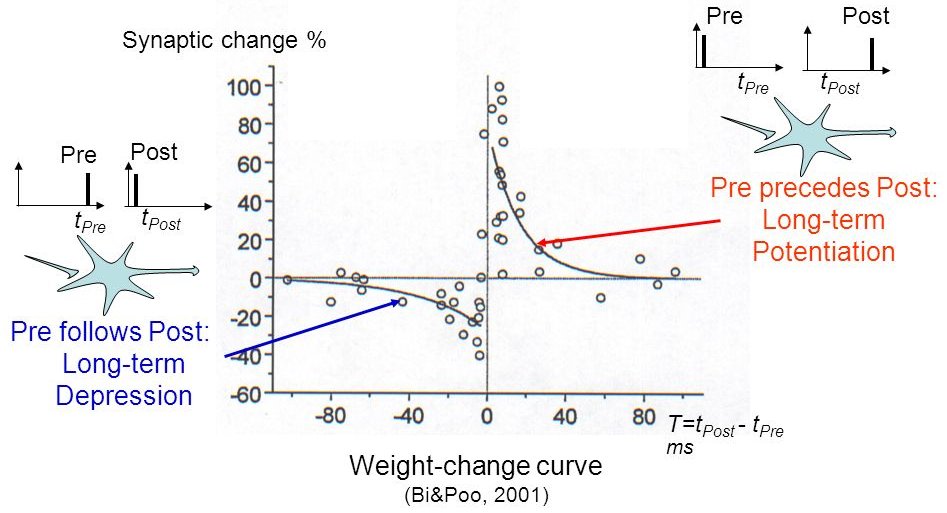
Bi and Poo (2001) Synaptic Modification by Correlated Activity: Hebb’s Postulate Revisited. Annual Review of Neuroscience 24.
STDP: Spike-timing dependent plasticity
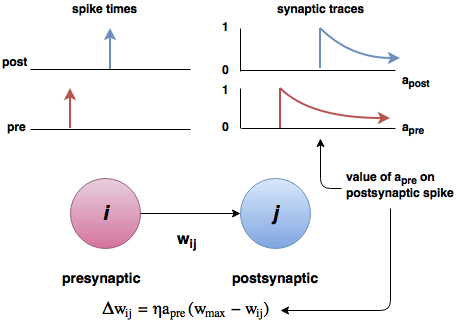
- The STDP (spike-timing dependent plasticity, Bi and Poo, 2001) plasticity rule describes how the weight of a synapse evolves when the pre-synaptic neuron fires at t_\text{pre} and the post-synaptic one fires at t_\text{post}.
\frac{dw}{dt} = \begin{cases} A^+ \, \exp - \frac{t_\text{pre} - t_\text{post}}{\tau^+} \; \text{if} \; t_\text{post} > t_\text{pre}\\ \\ A^- \, \exp - \frac{t_\text{pre} - t_\text{post}}{\tau^-} \; \text{if} \; t_\text{pre} > t_\text{post}\\ \end{cases}
STDP can be implemented online using traces.
More complex variants of STDP (triplet STDP) exist, but this is the main model of synaptic plasticity in spiking networks.
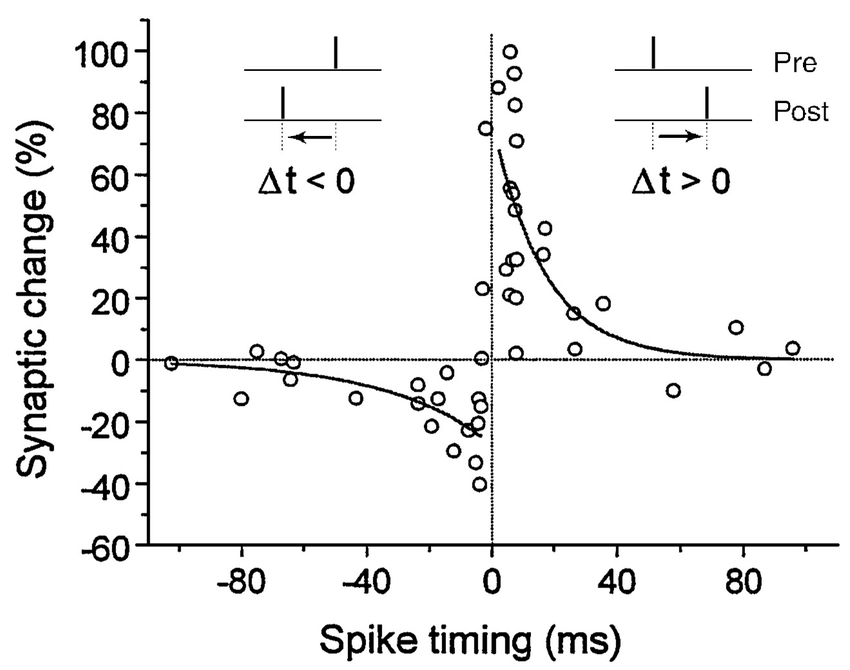
Bi and Poo (2001) Synaptic Modification by Correlated Activity: Hebb’s Postulate Revisited. Annual Review of Neuroscience 24.
Neuro-computational modeling
Populations of neurons can be combined in functional neuro-computational models learning to solve various tasks.
Need to implement one (or more) equations per neuron and synapse. There can thousands of neurons and millions of synapses, see Teichmann et al. (2021).
2 - Neuro-simulator ANNarchy
Neuro-simulators
Fixed libraries of models
NEURON
https://neuron.yale.edu/neuron/- Multi-compartmental models, spiking neurons (CPU)
NEST
https://nest-initiative.org/- Spiking neurons (CPU)
GeNN
https://genn-team.github.io/genn/- Spiking neurons (GPU)
Auryn
https://fzenke.net/auryn/doku.php- Spiking neurons (CPU)
Code generation
Brian
https://briansimulator.org/- Spiking neurons (CPU)
Brian2CUDA
https://github.com/brian-team/brian2cuda- Spiking neurons (GPU)
ANNarchy
https://github.com/ANNarchy/ANNarchy- Rate-coded and spiking neurons (CPU, GPU)
ANNarchy (Artificial Neural Networks architect)
Vitay et al. (2015)
ANNarchy: a code generation approach to neural simulations on parallel hardware.
Frontiers in Neuroinformatics 9. doi:10.3389/fninf.2015.00019
Installation
Installation guide: https://annarchy.github.io/Installation/
Using pip:
From source:
Requirements (Linux and MacOS):
- g++/clang++
- python >= 3.10
- numpy
- sympy
- nanobind
Features
Simulation of both rate-coded and spiking neural networks.
Only local biologically realistic mechanisms are possible (no backpropagation).
Equation-oriented description of neural/synaptic dynamics (à la Brian).
Code generation in C++, parallelized using OpenMP on CPU and CUDA on GPU (MPI is coming).
Synaptic, intrinsic and structural plasticity mechanisms.
Structure of a script
import ANNarchy as ann
# Create network
net = ann.Network()
# Create neuron and synapse types for transmission and/or plasticity
neuron = ann.Neuron(...)
stdp = ann.Synapse(...)
# Create populations of neurons
pop = net.create(1000, neuron)
# Connect the populations through projections
proj = net.connect(pop, pop, 'exc', stdp)
proj.fixed_probability(weights=ann.Uniform(0.0, 1.0), probability=0.1)
# Generate and compile the code
net.compile()
# Simulate for 1 second
net.simulate(1000.)3 - Rate-coded networks
Echo-State Network
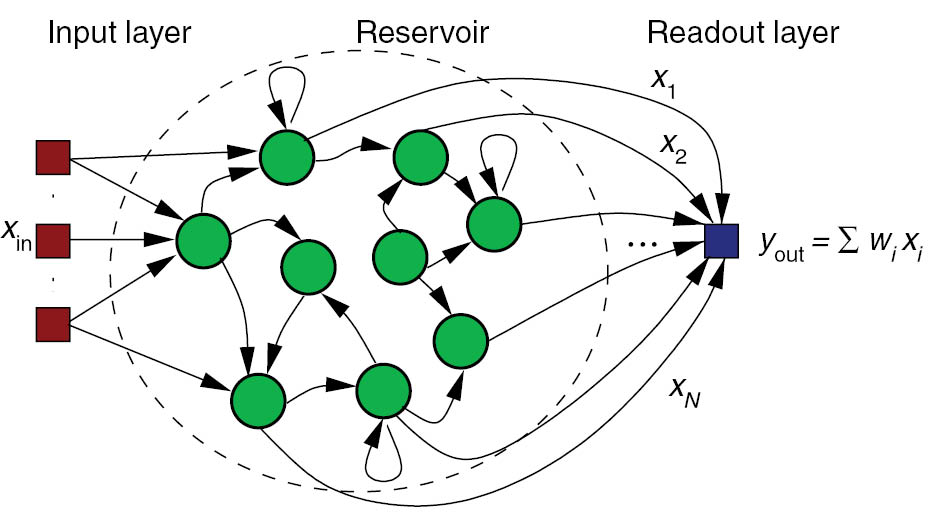
- ESN rate-coded neurons follow first-order ODEs:
\tau \frac{dx(t)}{dt} + x(t) = \sum w^\text{in} \, r^\text{in}(t) + g \, \sum w^\text{rec} \, r(t) + \xi(t)
r(t) = \tanh(x(t))
- Neural dynamics are described by the equation-oriented interface:
Parameters
- The parameters are provided as a dictionary:
Parameters can have one value per neuron in the population (local) or be common to all neurons of the population (global).
The parameters are considered global by default. To define a local parameters, use
ann.Parameter():
- Parameters and variables are floats by default, but the type can also be specified (
int,bool).
Variables
- Variables are evaluated at each time step in the order of their declaration.
The output variable of a rate-coded neuron must be named
r.Variables can be updated with assignments (
=,+=, etc) or by defining first order ODEs.The math C library symbols can be used (
tanh,cos,exp, etc).Initial values can be specified by using an
ann.Variable()object (default: 0.0).
- Lower/higher bounds on the values of the variables can be set with the
min/maxflags:
- Additive noise can be drawn from several distributions, including
Uniform,Normal,LogNormal,Exponential,Gamma…
ODEs
- First-order ODEs are parsed and manipulated using
sympy:
- The generated C++ code applies a numerical method (fixed step size
dt) for all neurons:
Several numerical methods are available:
- Explicit (forward) Euler (default):
- Implicit (backward) Euler:
- Exponential Euler (exact for linear ODE):
- Midpoint (RK2):
- Runge-Kutta (RK4):
- Event-driven (spiking synapses):
Network
Networkis the main object in ANNarchy:
- It is the container for all populations and projections of the network:
- It stores the configuration of the simulation, including the numerical time step
dtand the seed of the RNG:
- For better re-usability, you can create your own
Networksubclasses:
Networksubclasses allow to run simulations in parallel.
Populations
- Populations are creating by specifying a number of neurons and a neuron type:
- For visualization purposes or when using convolutional layers, a tuple geometry can be passed instead of the size:
- All parameters and variables become attributes of the population (read and write) as numpy arrays:
- Slices of populations are called
PopulationViewand can be addressed separately:
Projections
- Projections connect two populations (or views) in a uni-directional way.
Each target (
'exc', 'inh', 'AMPA', 'NMDA', 'GABA') can be defined as needed and will be treated differently by the post-synaptic neurons.The weighted sum of inputs for a specific target is accessed in the equations by
sum(target):
- It is therefore possible to model modulatory effects, divisive inhibition, etc.
Connection methods
Projections must be populated with a connectivity matrix (who is connected to who), a weight
wand optionally a delayd(uniform or variable).Several patterns are predefined:
proj.all_to_all(weights=ann.Normal(0.0, 1.0), delays=2.0, allow_self_connections=False)
proj.fixed_probability(probability=0.2, weights=1.0)
proj.one_to_one(weights=1.0, delays=ann.Uniform(1.0, 10.0))
proj.fixed_number_pre(number=20, weights=1.0)
proj.fixed_number_post(number=20, weights=1.0)
proj.gaussian(amp=1.0, sigma=0.2, limit=0.001)
proj.dog(amp_pos=1.0, sigma_pos=0.2, amp_neg=0.3, sigma_neg=0.7, limit=0.001)- But you can also load Numpy arrays or Scipy sparse matrices. Example for synfire chains:
Compiling and running the simulation
- Once all populations and projections are created inside a network, you have to generate to the C++ code and compile it:
You can now manipulate all parameters/variables from Python.
A simulation is simply run for a fixed duration in milliseconds with:
- You can also run a simulation until a criteria is filled (e.g. first-spike), see:
https://annarchy.github.io/manual/Network.html#early-stopping
Monitoring
By default, a simulation is run in C++ without interaction with Python.
You may want to record some variables (neural or synaptic) during the simulation with a
Monitor:
- After the simulation, you can retrieve the recordings with:
Calling get() flushes the underlying arrays.
Recording projections can quickly fill up the RAM…
Notebook: Echo-State Network
\tau \frac{dx(t)}{dt} + x(t) = \sum_\text{input} W^\text{IN} \, r^\text{IN}(t) + g \, \sum_\text{rec} W^\text{REC} \, r(t) + \xi(t)
r(t) = \tanh(x(t))

Jaeger (2001) The “echo state” approach to analysing and training recurrent neural networks. Jacobs Universität Bremen.
Plasticity in rate-coded networks
Synapses can also implement plasticity rules that will be evaluated after each neural update.
Example of the Intrator & Cooper BCM learning rule:
\Delta w = \eta \, r^\text{pre} \, r^\text{post} \, (r^\text{post} - \mathbb{E}[(r^\text{post})^2])
Each synapse can access pre- and post-synaptic variables with
pre.andpost..The
semigloballocality allows to do computations only once per post-synaptic neuron.pspoptionally defines what will be summed by the post-synaptic neuron (e.g.psp = "w * log(pre.r)").
Plastic projections
- The synapse type just has to be passed to
Network.connect():
- Synaptic variables can be accessed as lists of lists for the whole projection:
or for a single post-synaptic neuron:
Notebook: IBCM learning rule
Variant of the BCM (Bienenstock, Cooper, Munro, 1982) learning rule.
The LTP and LTD depend on post-synaptic activity: homeostasis.
\Delta w = \eta \, r^\text{pre} \, r^\text{post} \, (r^\text{post} - \mathbb{E}[(r^\text{post})^2])
Intrator and Cooper (1992) Objective function formulation of the BCM theory of visual cortical plasticity: Statistical connections, stability conditions. Neural Networks, 5(1).
Notebook: Reward-modulated RC network of Miconi (2017)
e_{i, j}(t) = e_{i, j}(t-1) + (r_i (t) \, x_j(t))^3
\Delta w_{i, j} = - \eta \, e_{i, j}(T) \, (R - R_\text{mean})
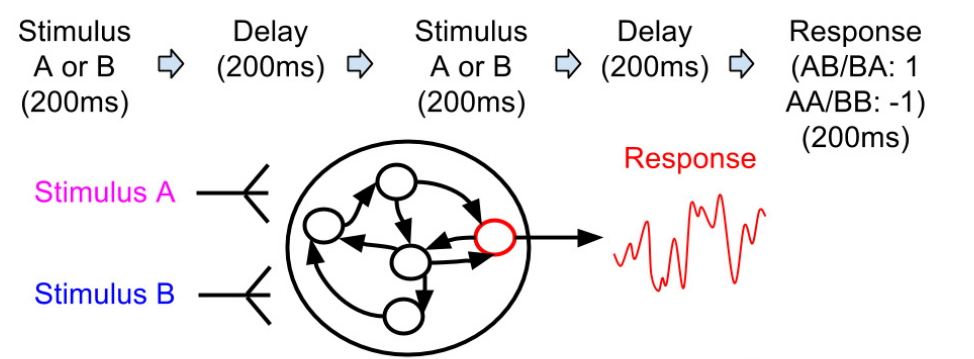
Miconi (2017) Biologically plausible learning in recurrent neural networks reproduces neural dynamics observed during cognitive tasks. eLife. doi:10.7554/eLife.20899
4 - Spiking networks
Spiking neurons
Spiking neurons must also define two additional fields:
spike: condition for emitting a spike.reset: what happens after a spike is emitted (at the start of the refractory period).
A refractory period in ms can also be specified.

- Example of the Leaky Integrate-and-Fire:
C \, \frac{d v(t)}{dt} = - g_L \, (v(t) - V_L) + I(t)
\text{if} \; v(t) > V_T \; \text{emit a spike and reset.}
Notebook: AdEx neuron - Adaptive exponential Integrate-and-fire
\tau \cdot \frac{dv (t)}{dt} = E_l - v(t) + g_\text{exc} (t) \, (E_\text{exc} - v(t)) + g_\text{inh} (t) \, (E_\text{inh} - v(t)) + I(t)

Brette and Gerstner (2005) Adaptive Exponential Integrate-and-Fire Model as an Effective Description of Neuronal Activity. Journal of Neurophysiology 94.
Conductances / currents
- A pre-synaptic spike arriving to a spiking neuron increases the conductance/current
g_target(e.g.g_excorg_inh, depending on the projection).
Each spike increments instantaneously
g_targetfrom the synaptic efficiencywof the corresponding synapse.This can be changed through the
pre_spikeargument of the synapse model:
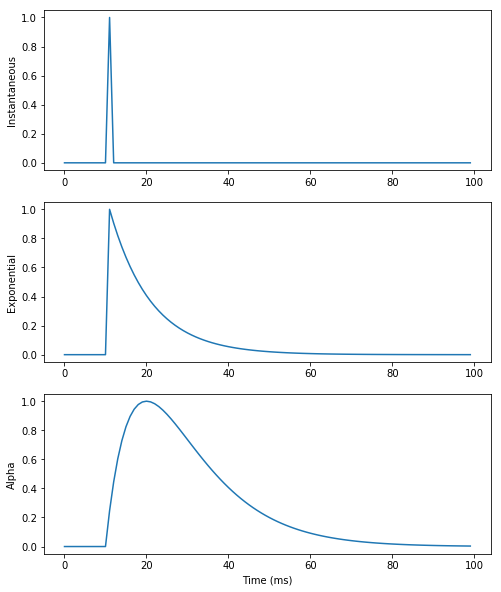
Conductances / currents
- For exponentially-decreasing or alpha-shaped synapses, ODEs have to be introduced for the conductance/current.
- The exponential numerical method should be preferred, as integration is exact.

Notebook: Synaptic transmission
equations = [
# Membrane potential
'tau*dv/dt = (E_L- v) + g_a + g_b + alpha_c',
# Exponentially decreasing
ann.Variable(
'tau_b * dg_b/dt = -g_b',
method='exponential'
),
# Alpha-shaped
ann.Variable(
'tau_c * dg_c/dt = -g_c',
method='exponential'
),
ann.Variable('''
tau_c * dalpha_c/dt =
exp((tau_c - dt/2.0)/tau_c) * g_c
- alpha_c''',
method='exponential'
),
],
Notebook: COBA - Conductance-based E/I network
\tau \, \frac{dv (t)}{dt} = E_l - v(t) + g_\text{exc} (t) \, (E_\text{exc} - v(t)) + g_\text{inh} (t) \, (E_\text{inh} - v(t)) + I(t)
Vogels and Abbott (2005) Signal propagation and logic gating in networks of integrate-and-fire neurons. The Journal of neuroscience 25.
Spiking synapses : Short-term plasticity (STP)
Spiking synapses can define a
pre_spikefield, defining what happens when a pre-synaptic spike arrives at the synapse.g_targetis an alias for the corresponding post-synaptic conductance: it will be replaced byg_excorg_inhdepending on how the synapse is used.By default, a pre-synaptic spike increments the post-synaptic conductance from
w, but this can be changed.
STP = ann.Synapse(
parameters = dict(
tau_rec = 100.0,
tau_facil = 0.01,
U = 0.5
),
equations = [
ann.Variable('dx/dt = (1 - x)/tau_rec', init = 1.0, method='event-driven'),
ann.Variable('du/dt = (U - u)/tau_facil', init = 0.5, method='event-driven'),
],
pre_spike="""
g_target += w * u * x
x *= (1 - u)
u += U * (1 - u)
"""
)Notebook: STP

Tsodyks and Markram (1997) The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. PNAS 94.
Spiking synapses : Example of Spike-Timing Dependent plasticity (STDP)
post_spikesimilarly defines what happens when a post-synaptic spike is emitted.
STDP = ann.Synapse(
parameters = dict(
tau_plus = 20.0, tau_minus = 20.0,
A_plus = 0.01, A_minus = 0.01,
w_min = 0.0, w_max = 1.0,
),
equations = [
ann.Variable('tau_plus * dx/dt = -x', method='event-driven'), # pre-synaptic trace
ann.Variable('tau_minus * dy/dt = -y', method='event-driven'), # post-synaptic trace
],
pre_spike="""
g_target += w
x += A_plus * w_max
w = clip(w + y, w_min , w_max)
""",
post_spike="""
y -= A_minus * w_max
w = clip(w + x, w_min , w_max)
""")Notebook: STDP
\begin{cases} \tau^+ \, \dfrac{d x(t)}{dt} = - x(t) \\ \\ \tau^- \, \dfrac{d y(t)}{dt} = - y(t) \\ \end{cases}
Bi and Poo (2001) Synaptic Modification by Correlated Activity: Hebb’s Postulate Revisited. Annual Review of Neuroscience 24.
And much more…
Standard populations (
SpikeSourceArray,TimedArray,PoissonPopulation,HomogeneousCorrelatedSpikeTrains), OpenCV bindings.Standard neurons:
- LeakyIntegrator, Izhikevich, IF_curr_exp, IF_cond_exp, IF_curr_alpha, IF_cond_alpha, HH_cond_exp, EIF_cond_exp_isfa_ista, EIF_cond_alpha_isfa_ista
Standard synapses:
- Hebb, Oja, IBCM, STP, STDP
Parallel simulations with
parallel_run.Convolutional and pooling layers.
Hybrid rate-coded / spiking networks.
Structural plasticity.
BOLD monitors.
Tensorboard visualization.
ANN (keras) to SNN conversion tool.






